Properties of an Elliptical Area
This tool calculates the basic geometric properties of an elliptical area. Enter the shape dimensions α and b below. The calculated results will have the same units as your input. Please use consistent units for any input.
α = | |||
b = | |||
Geometric properties: | |||
Area = | |||
Circumference = | |||
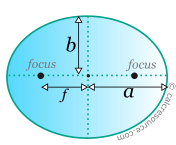
f = | |||
ε = | |||
κmax = | |||
 |
ADVERTISEMENT
Definitions
Geometry
The ellipse is a curved, closed, planar shape with two perpendicular axes of symmetry: major and minor. The definitions shown in the figure below are used:
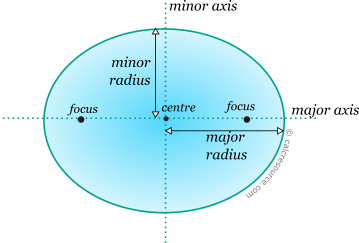
The points (x,y) of the circumference, assuming axis X is parallel to major axis and Y parallel to minor, satisfy the equation:
where x0, y0 the coordinates of the centre of the ellipse and α,b its major and minor radius, respectively.
Along the major axis, two focal points exist, at equal distances from centre. For every point of the circumference, the sum of its distances, from the focal points is constant and equal to 2α, where α is the major radius. The distance between each focus and the centre is:
where a,b the major and minor axis radius, respectively.
The eccentricity ε of the ellipse is a measure that describes how much it deviates from a perfect circle. It is given by the following formula:
where α the major radius. From this definition, ε becomes 0 when the ellipse is perfectly circular (α=b) and close to unity when it is quite linear (α>>b).
The curvature of the ellipse is not the same for all its points. It is greater where the major axis crosses the circumference and lower where the minor axis does. For an arbitrary point (x,y) of the circumference (assuming for simplicity that the origin of X,Y axes coincide with centre of ellipse, and X is aligned with its major axis), the curvature is given by the formula:
where α,b the major and minor radius, respectively. The maximum curvature occurs at x=a, y=0. Substituting to the above equation, it is found:
On the other hand, the minimum curvature occurs at x=0, y=b, and is given by:
Area
The area A of an elliptical area, with major radius α and minor radius b, can be found with these formulas:
Circumference
For the circumference P of an ellipse there is no closed form solution. It can be calculated numerically, through a rapidly converging Gauss-Kummer series as:
where
The binomial coefficient in the above series, which includes the fractional term 1/2, can be expanded to:
where the notation denotes the nth falling power of x, which is defined as: for integer .
Approximations for the ellipse circumference include the following two empirical formulas by Ramanujan:
These approximations are very good for small values of h (i.e. when the ellipse is more circular in shape) with errors of order h6 and h10. They deteriorate slightly however for values of h close to unity, when the ellipse becomes linear.
In this page, the ellipse circumference is evaluated using the Gauss-Kummer series for a number of terms that achieve desired accuracy, depending on the number of the displayed significant digits.