Mass Moment of Inertia of a Triangle
If you are interested in the cross-sectional moment of inertia (also called 2nd moment of area) of a triangle, please use this calculator. The current page is about the mass moment of inertia.
This tool calculates the moment of inertia I of a triangle (triangular lamina). Enter the triangle height, 'h' and its mass 'm' below. The calculated results will have the same units as your input. Please use consistent units for all input.
h = | |||
m = | |||
The results are: | |||
Ix = | |||
Ix0 = | |||
Ix1 = | |||
 | |||
ADVERTISEMENT |
ADVERTISEMENT
Definitions
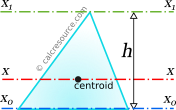
The moment of inertia of a triangular lamina, with respect to an axis passing through its centroid, parallel to its base, is given by the following expression:
where m is the mass of the object, b is the base width, and specifically the triangle side parallel to the axis.
The moment of inertia of a triangle with respect to an axis passing through its base, is given by the following expression:
This can be proved by application of the Parallel Axes Theorem (see below) considering that triangle centroid is located at a distance equal to h/3 from base.
The moment of inertia of a triangle with respect to an axis passing through its apex, parallel to its base, is given by the following expression:
Again, this can be proved by application of the Parallel Axes Theorem (see below), considering that triangle apex is located at a distance equal to 2h/3 from base.
Parallel Axes Theorem
The moment of inertia of any object, in respect to an arbitrary, non centroidal axis of rotation, can be found if its moment of inertia in respect to a centroidal axis, parallel to the first one, is known. The so-called Parallel Axes Theoremis given by the following equation:
where I' is the moment of inertia in respect to an arbitrary axis, I the moment of inertia in respect to a centroidal axis, parallel to the first one, d the distance between the two parallel axes and m the mass of the object.