Centroids - Reference Table
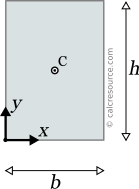
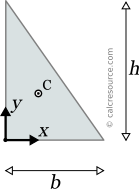
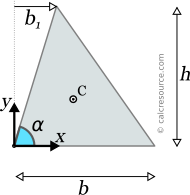
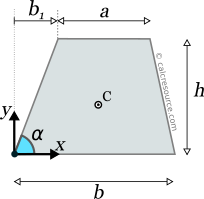
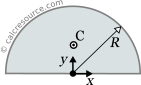
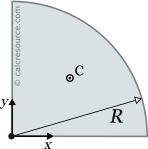
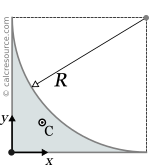
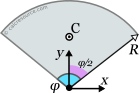
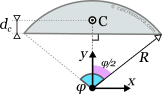
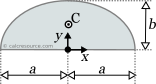
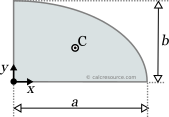
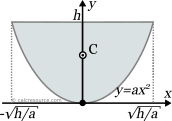
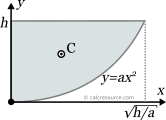
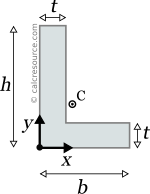
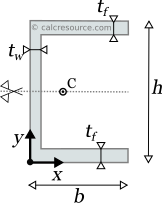
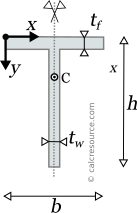
This page references the formulas for finding the centroid of several common 2D shapes. In the figures, the centroid is marked as point C. Its position can be determined through the two coordinates xc and yc , in respect to the displayed, in every case, Cartesian system of axes x,y. General formulas for the centroid of any area are provided in the section that follows the table.
Table of contents
Reference Table
Background
The centroid of an object represents the average location of all particles of the object. It can be defined for objects of any dimension, such as lines, areas, volumes or even higher dimension objects. It is a purely geometrical property, in contrast to the center of mass (also called center of gravity), which takes into account the mass distribution in the object. For objects with uniform mass distribution, the centroid is also the center of mass.
General formula for the centroid of an area
In the remaining we focus on the centroid of planar 2D areas. Being the average location of all points, the exact coordinates of the centroid can be found by integration of the respective coordinates, over the entire area. Specifically, the following formulas, provide the centroid coordinates xc and yc for an area A:
The integral term in the last two equations is also known as the static moment of area or first moment of area, S. Therefore these equations can be rewritten in this form:
where and .
Note, that the static moment of area is defined around an axis and conventionally the name of that axis becomes the index (e.g.: Sx is the 1st moment of area around axis x). It is not peculiar that the static moment, Sx is used for the centroid coordinate yc , since variable y is actually the measure of the distance from the x axis, thus the use of Sx.
Composite Areas
If an area is composed by a finite number n of simple subareas, with given centroid coordinates for each one of them, the first moments of area of the total area, can be found by summation of the respective static moments of the simple subareas. These are the equations:
where is the surface area of subarea i, and the centroid coordinates of subarea i.