Jump to
Table of Contents
Share this
Properties of a Circular sector
This tool calculates the basic geometric properties of a circular sector. Enter the shape dimensions R and φ below. The calculated results will have the same units as your input. Please use consistent units for any input.
R = | |||
φ = | |||
Geometric properties: | |||
Area = | |||
Perimeter = | |||
Arc length = | |||
rc = | |||
 |
ADVERTISEMENT
Table of Contents
Share this
Definitions
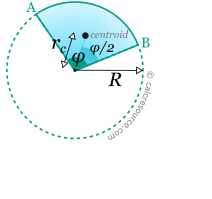
Geometry
The area A, the perimeter P and the arc length L of a circular sector, with radius R and central angle φ (in radians), can be found with these formulas:
The centroid (center of gravity) of the circular sector is located along the bisector of the central angle φ, at a distance from the centre equal to: