Properties of Octahedron
This tool calculates the basic geometric properties of a regular octahedron. Enter the shape dimension 'a' or 'h' below. The calculated results will have the same units as your input. Please use consistent units for any input.
Known data: | |||
Geometric properties: | |||
Volume = | |||
Surface area = | |||
Face area = | |||
Edge length = | |||
Inradius = | |||
Circumradius = | |||
Midradius = | |||
Dihedral angle (°) = | |||
Number of faces = | |||
Number of edges = | |||
Number of vertices = | |||
 |
ADVERTISEMENT
Definitions
Geometry
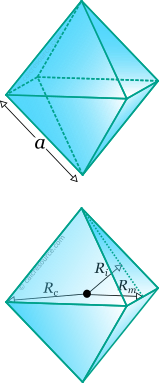
Octahedron is a regular polyhedron with eight faces. By regular is meant that all faces are identical regular polygons (equilateral triangles for the octahedron). It is one of the five platonic solids (the other ones are tetrahedron, cube, dodecahedron and icosahedron). It has 8 faces, 12 edges and 6 vertices.
The volume of a regular octahedron is given by the formula:
where the edge length.
The surface of one face as well, as the total surface area, is given by the following formulas:
The dihedral angle is defined as the interior angle between two adjacent faces of the polyhedron. For the regular octahedron it is given by the expression:
For any regular polyhedron, three spheres can be commonly defined: one that passes through all the vertices, called circumscribed sphere or circumsphere, one that passes through the centroids of all faces, called inscribed sphere or insphere, and one that passes through the middles of all edges, called midsphere. The radii of these spheres, circumradius , inradius and midradius , respectively, can be found for a regular octahedron, through the following expressions: