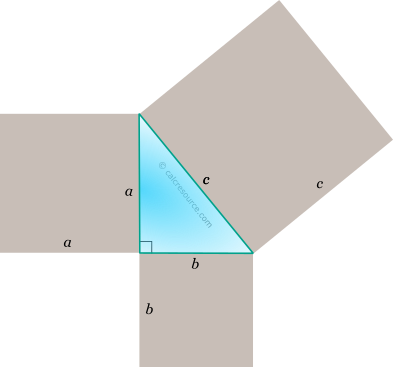
Properties of a Right Triangle
This tool calculates the basic geometric properties of a right triangle. Enter below the shape dimensions. The calculated results will have the same units as your input. Please use consistent units for any input.
Triangle defined by: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Geometric properties: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Area = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Perimeter = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Lengths: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Leg α = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Leg b = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Hypotenuse c = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Altitude h = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Angles : | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
φ = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
θ = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Circles | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Inradius r = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Circumradius R = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
ADVERTISEMENT
Definitions
Geometry
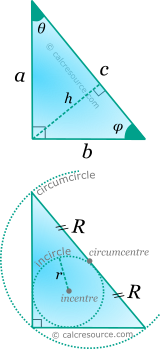
Right triangle is the triangle with one interior angle equal to 90°. Therefore two of its sides are perpendicular. These are the legs. The third side, which is the larger one, is called hypotenuse. All trigonometric functions (sine, cosine, etc) can be established as ratios between the sides of a right triangle (for angles up to 90°). Also, the right triangle features all the properties of an ordinary triangle. The following figure illustrates the basic geometry of a right triangle.
Here is a list of some prominent properties of right triangles:
- The sum of all three interior angles is 180°.
- The larger interior angle is the one included by the two legs, which is 90°.
- The sum of the two smaller interior angles is: . Therefore these are complementary angles. Knowing one, makes possible to find the other.
- A right triangle with equal legs (isosceles) has two interior angles equal to 45°.
- The side lengths are proportional to the sine of their opposite angles (law of sines). Therefore, hypotenuse is always the larger side.
- The altitude towards a leg coincides with the other leg.
- The area of a right triangle is the half product of the leg lengths: .
- The square of the hypotenuse is equal to the sum of the squares of the two legs: (Pythagorean Theorem).
- The hypotenuse of a right triangle is also a diameter of its circumcircle.
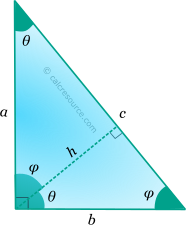
- The altitude towards the hypotenuse divides the right triangle into two daughter right triangles that are similar among each other and to the mother triangle.
- The altitude towards the hypotenuse divides it, into two smaller segments, that are proportional to the leg lengths. Also, divides the right angle of the mother triangle into angles φ, θ, equal to those included by the legs and the hypotenuse.
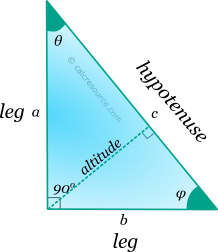
Trigonometry
The trigonometric functions -sine, cosine, tangent, cotangent- can be established as ratios of a right triangle side lengths. The following definitions can be made:
Circumcircle and incircle
There is a unique circle that passes through all triangle vertices, called circumcircle or circumscribed circle. For a right triangle, the hypotenuse is a diameter of its circumcircle. Therefore, the radius of circumcircle is:
There is also a unique circle that is tangent to all three sides of a right triangle, called incircle or inscribed circle. Its radius is given by the formula:
Altitude
Altitude towards a side of a triangle is the perpendicular segment to that side, beginning from the opposite vertex. Since, for a right triangle the two legs are perpendicular, it must be that, the altitude, towards any of the two legs, is the other leg. The altitude towards the hypotenuse can be found, considering that hypotenuse divides the right triangle into two daughter right triangles, and the trigonometric functions can be applied to any of them (see previous figure):
Area
The area of any triangle, having a side L and an altitude towards that edge, equal to H, can be found by the formula: . Applying this equation for one leg or for the hypotenuse of the right triangle, we find two equivalent expressions, for the calculation of its area:
The above expressions uncover another useful relationship for the sides α, b, c, and the altitude h, of a right triangle:
Pythagorean theorem
The Pythagorean Theorem (Pythagoras, 570-495 BC, proved it for first time), states that: the square of the largest side of a right triangle (hypotenuse) is equal to the sum of the squares of the two smaller sides (legs).
In symbolic form:
Pythagorean Theorem makes possible to find any side of a right triangle, when the other two are known. In the figure below, a visualization of the Pythagorean Theorem is shown. On each side of the triangle a square is drawn. According to the theorem, the area of the largest square (c2) is equal to the combined areas of the smaller ones (a2+b2).