CALC RESOURCE

x

Calculation options:

Number of digits:
10x notation for big numbers:

Properties of a Trapezoid

This tool calculates the basic geometric properties of a trapezoid. Enter below the shape dimensions. It is not required for base α to be the bigger one. The calculated results will have the same units as your input. Please use consistent units for any input.

α =
b =
h =
Additional input (select which):
Angle φ1 Angle φ2 Length α1 Length α2 Isosceles
φ1 =		deg rad
φ2 =		deg rad
α1 =
α2 =
Geometric properties:
Area =
Perimeter =
xc =
yc =
Lengths:
Side c =
Side d =
Diagonal p =
Diagonal q =
Angles :	deg rad
φ1 =
φ2 =
φ3 =
φ4 =

Definitions

Geometry

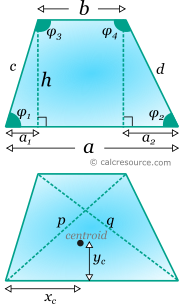
Trapezoid is a quadrilateral shape with at least two parallel sides. The definitions shown in the following figure are used:

The area of a trapezoid is given by the formula:

where a, b the lengths of the two bases and h the height.

The perimeter of a trapezoid is simply the sum of the lengths of all sides:

Finding the lengths of the non parallel sides c and d, can be done if one interior angle of the trapezoid is known. Let's assume that angle φ₁ is given. Using simple geometrical principles, for the right triangles, with sides c, d as hypotenuses (see figure below), the calculation of lengths c and d can by done:

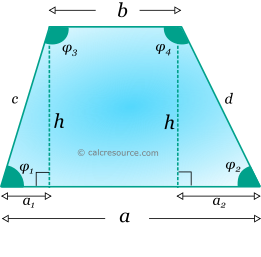
Interior angle φ₃ is supplementary with φ₁, since bases a and b are parallel. Therefore:

The remaining interior angles (which are also supplementary) can be found using simple geometrical principles, for the right triangle, with side d as hypotenuse:

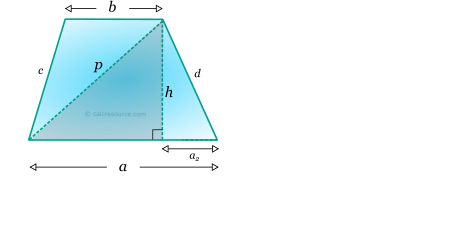
There are many ways to find the lengths of diagonals, once the sides or the interior angles are known. Here, a solution employing the Pythagorean Theorem on the highlighted right triangle (see next figure) is presented, for diagonal p:

Similarly, the other diagonal is found as:

Centroid

The centroid coordinates in respect to the bottom base left vertex, x_c and y_c (see figure below) can be calculated using the first moments of area, of the three sub-areas A,B,C.

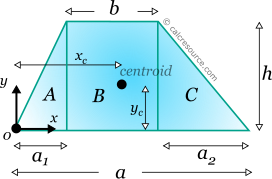
For x_c, considering the first moments of area, relative to the part B middle, it is found:

where A is the area of the trapezoid.

As for the y_c, considering the first moments of area relative to the bottom base, it is found:

The above formulas are valid even when α₁ or α₂ are negative, which occurs when the angles φ₁ or φ₂, are obtuse.